Introduction and rules

The blocked n-queen problem is a variant of the classic n-queen problem, with extra pieces, or “walls” on the board, restricting a queen’s vision. The goal is to put a certain number of queens on the board so that no two queens attack each other. A wall is an occupied tile which blocks a queen’s line of attack. Walls will be represented with a pawn, but note that the pawns cannot attack, they only function as blockers.

These are valid configurations, as the pawn blocks the line of attack between the queens.

However, this is an invalid configuration, as the queens can see each other diagonally.

You can play some selected configurations of this puzzle here.

Naming and conventions

An n-W board is a board with n walls. From here on out, we will only be discussing 8×8 boards (classical chess boards), so when a board is mentioned, a size of 8×8 is assumed. For example, a “3-W board” is an 8×8 board with 3 walls in it.

A solution of an n-W board is a board in which no queens are attacking each other – a “legal” board as per the rules.

The value of an n-W board is the maximum number of queens that can be fit in a valid configuration. For example, the value of the 0-W board, the empty chess board, is 8, as known from the classical 8-queen problem.

A solution is optimal if it’s a solution with value queens. For example, the basic 8-queen problem is known to have 92 optimal solutions – 92 solutions with 8 queens on the board.

Tiles in a board will be differentiated via 2 coordinates. The first one will be the row, going from 0 to 7 starting with the top row. The second one will be the column, going from 0 to 7 starting with the left column. For example, (1,1) will represent the following tile:

Research Approach

It is known that the classical, wall-free board has a value of 8. Adding the walls creates a huge amount of variants (2^n×n) for every size of board. Throughout this article I’ll investigate the relationship between the number of walls, their position, and the board’s value. I’ll also generate some interesting puzzles.

We’ll divide the analysis into three separate sections:

1.  collecting and saving solved puzzles for small values of n (The n-W board, its value, and an optimal solution)
2. answering some general questions about this problem, such as the minimum number of walls that allow for a certain number of queens.
3. Collecting a group of “interesting” boards (“interesting” to be defined later)

Before we go into analyzing boards in more depth, it’s important to develop an algorithmic approach to finding a board’s value. A constructive approach to this will also give us an example of an optimal solution.

There are many efficient algorithms developed for solving the classic n-queen problem (or, in our nomenclature, the 0-W board). A slight adaptation of many of these would probably work for our scenario as well – I decided to pose the problem as an integer linear programming (ILP) problem since it’s one of my areas of expertise.

I used the SCIP solver, alongside the ZIMPL language, a very strong tool to create easy to parametrize ILPs (or convex optimization problems in general). I created two different ILPs, which I’ll get into in more detail as they come up in the next sections. A full walkthrough of both ILPs, their variables and their constraints, can be found here.

Objective 1:
Finding a board’s value and optimal solutions

The first ILP, the Base Model (BM), requires the coordinates of the walls as an input, and gives out the board’s value alongside an optimal solution as output. Note that optimal solutions are not necessarily unique and this model will only output one. This model is made to have as few variables and constraints as possible, and to have constraints be as tight as possible, in order to easily solve many iterations of the problem later and be able to store the results.

The objective of the BM is simply to maximize the number of queens that can fit on the given board. Therefore, if the optimal solution to the ILP problem is found, that will count as proof that the value of the objective function is the board’s value. 

Representing boards and their solutions in a memory-efficient way

I used a bitboard method to represent the entirety of a board’s information – the position of the walls, the position of the queens of an optimal solution, and the board’s value. “Solved” boards will be represented with a 3-dimensional integer vector, with each coordinate representing the following:

• A 64-bit integer representing the positions of the walls. The indexing function simply follows the rows first and the columns second, lexicographically. So, the 8^th bit starting from the left is the (0,7) tile. The 9^th one would be the (1, 0) tile.
• A 64-bit integer representing the positions of the queens, for one of the board’s optimal solutions.
• An integer representing the board’s value. This is encoded within the previous coordinate (simply count the number of 1s in the 64-bit integer), but it is easier to just have it available separately.

Generating every 2-W board and their solutions

With a straightforward python script, I generated and iterated through every possible board with 2 walls in it – there are 2016 of them (all possible ways of picking 2 out of 64 tiles). The results are as follows:

Total 2W boards: 2016
Max 2W queens: 10
max 2W queen example board: ((1, 3), (2, 5))
There are 368 boards with 8 queens in them. (18.25%)
There are 1610 boards with 9 queens in them. (79.86%)
There are 38 boards with 10 queens in them. (1.88%)

You can directly see all the boards and their solutions in the project’s repository here. As one might expect, most boards allow for 9 queens to be on the board instead of 8. It’s interesting to see that there are 38 boards that allow for 10 – my expectation was that 9 would be the maximum, as with 8 queens on the board, any new queen would be attacked vertically and horizontally. However, that was not the case. Here is an example of a valid 10 queen configuration for the board with tiles (1,3) and (2,5) blocked:

Board Symmetries

Brrute forcing every single 2-W board is plausible, but starting from the 3-W and 4-W boards, it’s worth thinking about saving some computing power, as there are 41664 and 635376 possible configurations respectively, which would take a while to go through.

We can use the fact that a valid board will still be valid if we apply any symmetry to it. There are a total of 8 possible symmetries, grouped into reflection and rotation symmetries. The reflections are vertical, horizontal, or diagonal (main diagonal or anti diagonal). The rotations are 90°, 180°, 270°. The final symmetry is the identity (leaving the board as it is).

This means that we can group all boards by the equivalence class given by their symmetries without losing any complexity. Intuitively, this is easy to see. For the rotations, simply imagine grabbing the board and rotating it 90° to the right 4 times. Each rotation is a different board in terms of coordinates, but functionally it is the same. For the reflections, simply imagine mirroring the board across the respective line.

Following that logic, it’s trivial to see that the value of boards in the same symmetry equivalence class will be the same. From here on out, instead of looking at all boards, we will only be looking at one representative of each equivalence class.

Generating every 3-W board and their solutions

Total 3W boards: 41664
Symmetry classes checked: 5278
True boards checked: 41664/41664
Max 3W queens: 11
Max 3W queen example board: ((1, 4), (3, 1), (4, 3))
There are 294 boards with value 8. (5.57%)
There are 4291 boards with value 9. (81.30%)
There are 692 boards with value 10. (13.11%)
There is 1 board with value 11. (0.02%)

Another result that I didn’t expect – there is one singular 3-W board with value 11. If you account for all its symmetric partners, there are 8 possible boards. A very specific configuration seems to be required. Here it is:

It’s interesting to see that every queen is one horse jump away from at least 1 other queen. It might be the most efficient way to pack queens with the least number of walls. This pattern repeats itself in most optimal solutions for all boards.

Generating every 4-W board and their solutions

Total 4W boards: 635376
Symmetry classes checked: 79920
True boards checked: 635376/635376
Max 4W queens: 11
Max 4W queen example board: ((0, 0), (1, 3), (3, 4), (4, 1))
There are 1386 boards with value 8. (1.73%)
There are 48722 boards with value 9. (60.96%)
There are 29571 boards with value 10. (37.00%)
There are 241 boards with value 11. (0.30%)

Notably, 4-W boards still have a maximum value of 11. It’s interesting to see that the example board is one of the 11 value 3-W boards, with the top-left corner added to it – a tile that cannot influence a queen’s field of vision.

Objective 2

Least walls for number of queens

Using our previous methods, we can figure out the smallest number of walls needed for 8, 9, 10 and 11 queens. For 8 queens, the bare 0-W board works, as is known from the basic 8-queen problem. The first 9 queen solutions appear with 1 wall. Then, we have 10 queen solutions for 2-W boards, and 11 queen solutions for 3-W boards.

However, when checking the 4-W boards, no 12 queen solutions were found, meaning that at least 5 walls are needed for that to be feasible. Checking all 5-W boards isn’t reasonable because of the vast amount of possible configuration.

The second ILP, the Least Walls Model (LWM), flips the original problem to find that kind of solution. Given a number of queens, it finds the least number of walls that allows for a legal configuration with that number of queens, and a valid board with those criteria. Remember to check out this post for more details on the ILPs themselves.

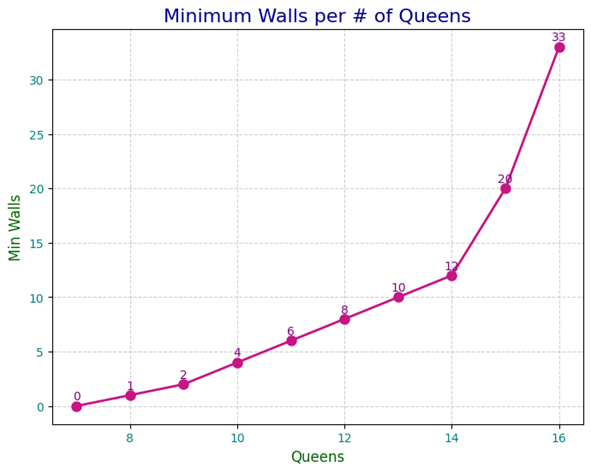
I ran the LWM for q = 12, 13, 14, 15 and 16 – our still unknown values that we have no hope of brute-forcing a solution for. Here’s a graph with the results:

Note that the graph cuts off at 16 because there is no way to put 17 queens on an 8×8 board while leaving at least one empty space between every queen, making the problem infeasible.

It’s interesting that adding a 4^th, 6^th, 8^th or 10^th wall does nothing, but a 12^th one does. I was curious to see how many 12-W boards with value 16 there were, so I did a small modification to the LWM to count all feasible solutions – and there are only 2, which is quite remarkable. Note that they are the same solution with the vertical reflection applied, so when looking at equivalence classes, the solution is unique in that sense.

7×7 Boards

I performed a similar analysis to the 8×8 board but for 7×7 boards. The results were surprisingly slightly different and way more restrictive. I ran the LWM starting from q=7, similar to above but starting with one less queen, as the 7×7 empty board allows for 7 queens to be placed. Here are the results:

There is no feasible way to put more than 16 queens on the board – just as for 8×8 boards. However, I did not expect there to be feasible ways to put 16 or even 15, but it seems like I was wrong. There are 36 20-W board with a value of 15, and exactly one 33-W board with a value of 16 – it is unique even accounting for symmetries.

Here’s the 33-W board:

It makes sense when you look at it. It’s simply the board with every tile blocked except for one of the basic 16 queen configurations.

Let’s look at one of the 20-W boards with value 15:

6×6 Boards

It is easy to see that there is no way to fit more than 10 queens in a 6×6 board without at least 2 of them being adjacent to each other. The smallest number of walls that allows for 9 queens is 6. Here is an example solution:

Objective 3:

Generating “interesting” puzzles

I want to find a certain subgroup of boards with “interesting” properties, which could make for fun to solve puzzles. I am looking for the following properties:

1. Unique optimal solution – If the board’s value is k, there should only be 1 valid configuration of k queens.
2. Minimum walls – Imagine a 3-W board with value 11. Since we know that no 4-W boards have value 12, you could fill any empty tile with a wall and it wouldn’t change the validity of the puzzle. The 3-W version is the minimal version, ensuring that there are no duplicates. If adding a 4^th wall did allow for an extra queen, then it would be considered a different puzzle. There is an edge case where adding an extra wall could force the uniqueness of the solution. In that case, the version with the extra wall is considered the minimum.
3. Grouped by symmetry – Only one puzzle per symmetry group will be preserved. Reflection symmetries will be grouped as well (Horizontal/Vertical/Diagonals)

A note on symmetry and uniqueness

If a wall configuration makes the board invariant to some symmetry, this can mess with the solution uniqueness, because you can apply the rotation or reflection to a solution and have another valid solution. For example, this 2-W board with value 10 has 2 optimal solutions:

The walls are invariant to the main diagonal symmetry. So the different solutions are actually applications of the symmetry that the walls are invariant to. The structure of these solutions is the same, but for now, I will not consider these for the “interesting” puzzle subset.

Algorithmic approach to finding interesting puzzles

I wrote a quick script to find all puzzles fitting the interesting criteria with between 2 and 4 walls. It is fairly slow so going further than that isn’t reasonable without optimizing the algorithm or getting more computing power. The algorithm iterates through all n-W boards for a certain n, and does the following:

1. Find board’s value (run BM)
2. check if a smaller board with walls contained in the n-W board’s walls with the same value was already found. If so, skip this one.
3. Run a modified BM that counts optimal solutions, to check if 2 or more solutions exist
4. if they don’t, save board (and track symmetries)

I used the script to come up with 1000 puzzles with unique optimal solutions for their board values. This includes all such 2-W and 3-W puzzles (about 250 meet the criteria), and only some of the 4-W ones. They are the puzzles that can be played here.

Future Research:

There are a few more things I’d like to do in regards to this problem in the future.

1. Analyze bigger boards – in particular, how a bigger board size impacts the “most queens with least walls” optimization problem.
2. Extend the “interesting” puzzle database to include puzzles with 5 or more walls, developing a more efficient approach to generating them. Also include different board sizes.