Compacted Dominoes: Optimal Solutions

Some decades ago, my dad Eduardo wrote an article about a certain domino tiling game, which he named Compacted Dominoes. He recently revisited it, writing about it in his blog, and implementing a playable version (Note that these posts are in Spanish). I recommend reading through his post if you can, but let’s take a look at the game’s rules and the underlying problem it’s trying to solve.

Formulation

Utilizing my father’s terminology, let’s define the Domino-n set as the set of all domino pieces with numbers from 0 to n.

$\displaystyle \text{Domino-}n = \{ (a, b) \mid 0 \le a \le b \le n \}$

Let’s consider the square grid. The game’s objective is to place down all the domino pieces on the grid, with a twist. Two pieces can overlap if they share a number in a given square. For example, the following image:

We can see a tiling which contains the dominoes (0,1) and (0,2). The pieces overlap in the zero square.

The objective of the Domino-n game is to find a tiling which contains all pieces of the Domino-n set (from here on, a solution) and has the smallest area possible. Or in other words, finding the minimum number of squares in the grid necessary to be able to lay down all the pieces.

In this post, I’ll explore optimal solutions for specific values of n using both mathematical reasoning and computational methods.

Computational complexity

The problem of finding an optimal solution has two layers. On one hand, a solution with the smallest possible area must be found. And on the other hand, it must be proven that a solution with a smaller area cannot exist. The great computational difficulty of this problem comes from this second part.

For example, imagine trying to prove that no solutions of area 17 exist for the Domino-6 game. Each square has 7 options of numbers, from 1 to 7. This already gives you ~2.3 x 10ˆ14 possible solutions, and we haven’t even looked at the possible configurations of 17 squares on the grid, of which there are a lot, and they accumulate multiplicatively. So it’s not possible to brute-force this search.

To give a little bit of mathematical context (although not rigorous). The problem is very similar to certain graph coloring problems (imagine that the numbers of the domino pieces are colors. There is no difference between considering 0, 1 and 2, or green blue and red).

It is known that this type of optimization problem is computationally “difficult”, in a technical sense. Even with strong optimization software/solvers, this type of problem can be very hard to solve. It’s necessary to find some way to bound the search space.

Solving

With that in mind, we divide the solving of the Domino-n area minimization problem into two phases:

The first phase, with a mathematical approach, will be to find a strong lower bound for the area of an optimal solution for Domino-n. We will prove that, for the Domino-n game, the area A of a solution must be greater than or equal to a certain function m(n).

The second phase, with a computational approach, will be to find solutions with area m(n), for certain values of n. Since there cannot exist a solution with a lower area, it wil lbe proven that that is the minimum possible area for the Domino-n game. There is a small exception for Domino-7 which will be covered later as well.

Lower Bound

To recap, we’re looking for a way to get a lower bound of the area of a solution S for Domino-n. Let’s start by defining a couple of auxiliary terms and formulas:

A(S) = Area of solution S (number of occupied squares in the grid)
Ad(S) = Number of internal adjacencies of S
P(S) = Perimeter of solution S

A quick run-down of the perimeter value:

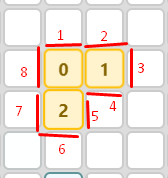
The perimeter of this shape is 8. It is the number of connections between the shape and unoccupied squares.

The number of internal adjacencies of S is the number of internal connections of the shape. For example, our shape has 2 internal adjacencies:

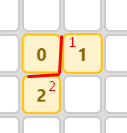
If we consider the fact that every square on the grid is connected to 4 other squares, we get the following formula, which is valid for any solution S. We will call this Formula A.

$\displaystyle 4\,A(S) = 2\,Ad(S) + P(S)$

The formula is quite intuitive. The solution has A(S) squares. Each one of those has 4 connections, giving us a total of 4 * A(S) connections related to S (the left-hand side). Some of these connections are on the border of S: these are exactly the perimeter P(S) as defined above. The rest are, by definition, not connected to an unoccupied square, or they would be counted in the perimeter term. So they are internal adjacencies. Each internal adjacency must be counted twice, since it connects exactly two squares of S. This gives us the right-hand side of formula A, 2 * Ad(S) + P(S).

Why look at internal adjacencies: The domino-6, for example, has 28 domino pieces that must be laid down. Each piece takes 2 squares. Meaning that, for each piece that you want to lay down, at least one internal adjacency is required in the solution. So, for a solution S of domino-6, the shape of the solution must allow for at least 28 internal adjacencies.

Generalizing, the number of pieces to lay down for Domino-n is:

$\textstyle \tbinom{n+1}{2} + (n+1)$

So we know that, given a solution S, the following inequality must hold:

$\displaystyle Ad(S) \ge \binom{n+1}{2} + (n+1)$

Due to Formula A, we know that:

$\displaystyle Ad(S) = 2A(S) - \frac{P(S)}{2}$

Putting these together, and solving for A(S), we reach what we’ll call Formula B:

$\displaystyle A(S) \ge \frac{\binom{n+1}{2} + (n+1)}{2} + \frac{P(S)}{4}$

To further improve this bound, we’ll also bound the perimeter of a solution S.

Consider R(S), the smallest rectangle which contains the solution. That is, the rectangle with the smallest area which contains the entire shape of S. For example, for our shape:

The 2×2 square is the smallest rectangle which contains it.

Two results about R(S):

The area of R(S) is greater than or equal to the area of S, as S is contained in R(S).
The perimeter of S is greater than or equal to the perimeter of R(S). This is a bit harder to visualize, but it comes from the fact that S has at least 2 borders per row and 2 borders per column, whereas the rectangle has exactly 2. It is left as an exercise to the reader to fully convince themselves of this.

So, if we consider:
w = width of the rectangle
h = height of the rectangle
We get:

$w h \ge A(S) \quad , \quad P(S) \ge 2(w+h)$

Let’s think about all the possible minimal rectangles for a solution S of area A(S). Without loss of generality, we can assume that S has a single connected component (no pieces that aren’t connected to the rest), and we can take one single representative of each symmetry class.

So, it becomes clear that the possible values of w and h are:

$\textstyle w\in{1,\dots,A(S)},\quad h=\big\lceil\tfrac{A(S)}{w}\big\rceil,\quad w,h\in\mathbb{Z}_{>0}$

Putting all of these factors together, we can get a bound for the perimeter of a solution S:

$\displaystyle P(S) \ge P(R(S)) \ge 2 \min_{1 \le w \le A(S)} \Big( w + \left\lceil \frac{A(S)}{w} \right\rceil \Big)$

With this, we can go back to Formula B with more tools:

$\displaystyle A(S) \ge \frac{\binom{n+1}{2} + (n+1)}{2} + \min_{1 \le w \le A(S)} \frac{ w + \left\lceil \frac{A(S)}{w} \right\rceil }{2}$

Reorganizing, we get the following:

$\textstyle 2\,A(S) - \min_{1 \le w \le A(S)} \left( w + \left\lceil \frac{A(S)}{w} \right\rceil \right) \ge \binom{n+1}{2} + (n+1)$

This gives us a good lower bound for the area of a solution of the Domino-n game. We can finally define the function m(n).

$\displaystyle m(n) = \min \Big\{ a \in \mathbb{N} \;\Big|\; 2\,a - \min_{1 \le w \le a} \Big( w + \left\lceil \frac{a}{w} \right\rceil \Big) \ge \binom{n+1}{2} + (n+1) \Big\}$

For each natural number n, this gives us the smallest area which satisfies our established bound. In other words, any solution must have an area greater than or equal to m(n). Some values of m(n):

n	m(n)
5	15
6	19
7	23
8	28
9	34
10	40

And a graph for the function for n ranging from 1 to 100:

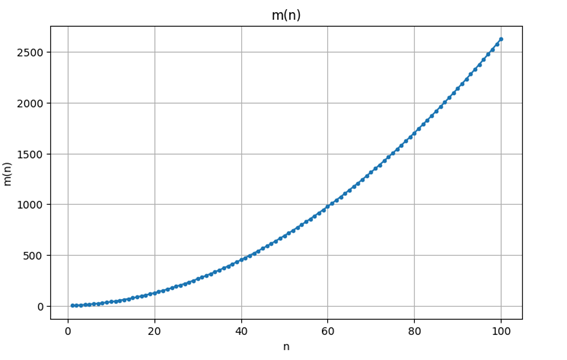
Now that we have this lower bound, if we were able to get a solution of area m(n) for each n, we would instantly know that it is optimal.

Solution search

The solution search was coded as a constraint programming problem, using MiniZinc with Google OR-Tools as a solver. The code can be found in this git repository, alongside relevant documentation. Everything was ran on my personal home computer, with runs ranging from a few seconds to several hours for larger values of n. This configuration was used in MiniZinc:

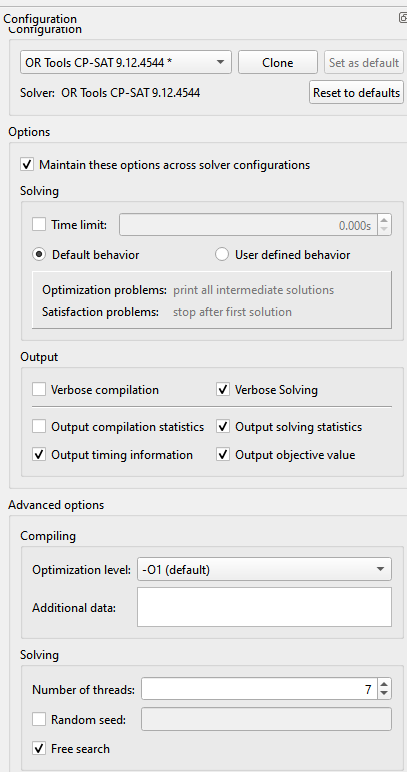
For almost every value of n up to 10, a solution of area m(n) exists. I will now proceed to list those solutions for n between 6 and 10, as the previous ones are easy to find.

A note: It is not true that a solution of area m(n) exists for every value of n. For example, m(7) = 23, but a solution of area 23 cannot exist for the Domino-7 game. The smallest possible area is 24, which does exist. This is due to a different combinatorial lower bound. In order to have a solution for Domino-7, each number must be connected to at least 7 other numbers, and to itself. To do this, you need at least 3 squares occupied with each number, giving you a minimum of 3*8 = 24 squares.

Solution listing

n = 6

The value of m(6) is 19. A solution of area 19 exists, which is therefore optimal.

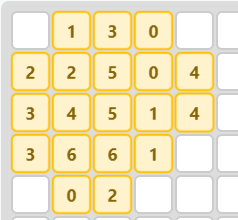
Import-ready version:

| 0, 2, 4, 1, 0
| 3, 3, 6, 1, 5
| 4, 5, 6, 2, 5
| 4, 7, 7, 2, 0
| 0, 1, 3, 0, 0

n = 7

The value of m(7) is 23. A solution of area 23 doesn’t exist. 24 is the minimum due to the argument given above.

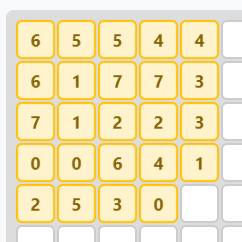
Import-ready version:

| 7, 6, 6, 5, 5
| 7, 2, 8, 8, 4
| 8, 2, 3, 3, 4
| 1, 1, 7, 5, 2
| 3, 6, 4, 1, 0

n = 8

The value of m(8) is 28. A solution of area 28 exists, which is therefore optimal.

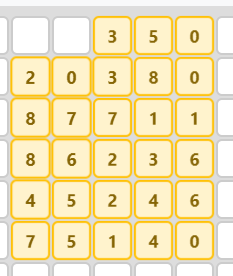
Import-ready version:

| 0, 0, 0, 0, 4, 6, 1
| 0, 0, 3, 1, 4, 9, 1
| 0, 0, 9, 8, 8, 2, 2
| 0, 0, 9, 7, 3, 4, 7
| 0, 0, 5, 6, 3, 5, 7
| 0, 0, 8, 6, 2, 5, 1
| 0, 0, 0, 0, 0, 0, 0

n = 9

The value of m(9) is 34. A solution of area 34 exists, which is therefore optimal.

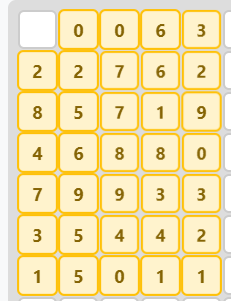
Import-ready version:

| 0, 1, 1, 7, 4
| 3, 3, 8, 7, 3
| 9, 6, 8, 2, 10
| 5, 7, 9, 9, 1
| 8, 10, 10, 4, 4
| 4, 6, 5, 5, 3
| 2, 6, 1, 2, 2

n = 10

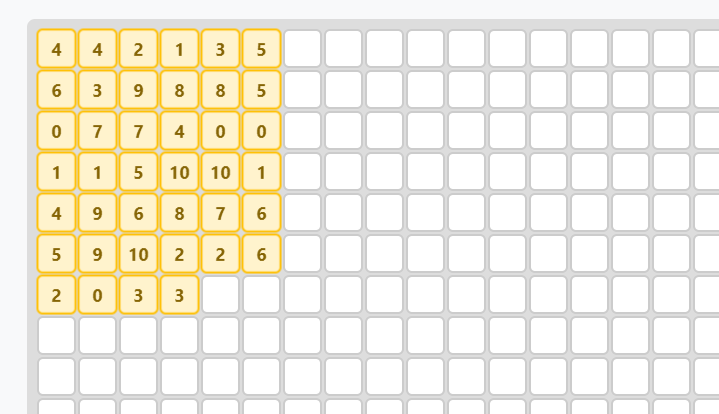
The value of m(10) is 40. A solution of area 40 exists, which is therefore optimal.

Import-ready version:

| 5, 5, 3, 2, 4, 6
| 7, 4, 10, 9, 9, 6
| 1, 8, 8, 5, 1, 1
| 2, 2, 6, 11, 11, 2
| 5, 10, 7, 9, 8, 7
| 6, 10, 11, 3, 3, 7
| 3, 1, 4, 4, 0, 0

Next steps

For values of n greater than 10, the solution search for solutions of area m(n) rapidly grows in difficulty. I have the following conjecture:

For all n ≥ 8, there is a solution for Domino-n with area m(n), which is therefore optimal.

In other words, m(n) is not just a lower bound for the area, but directly gives the minimum area for the Domino-n game. Intuitively this seems true, because for large values of n, the m(n) bound is much stronger than the combinatorial bound which wins over it for n = 7. However, I haven’t been able to prove it yet. There doesn’t seem to be an easy way to build solutions from smaller solutions, or other similar tools.

Another interesting experiment would be to find optimal solutions for n between 11 and 20, which seems computationally reachable if given enough time.

Formulation

Computational complexity

Solving

Lower Bound

Solution search

Solution listing

n = 6

n = 7

n = 8

n = 9

n = 10

Next steps

Leave a Reply Cancel reply