Dominó Compactado: Soluciones Óptimas

Hace algunas décadas, mi papá Eduardo escribió un artículo sobre un cierto juego de teselado de dominós, que llamó Dominó Compactado. Recientemente volvió a mirarlo, y escribió sobre el tema en su blog, implementando una versión jugable. Recomiendo leer el post, pero veamos rápidamente una formulación del juego y del problema de fondo que busca resolver.

Formulación

Usando la nomenclatura de mi padre, llamemos Dominó-n al conjunto de todas las piezas de dominó con números 0 a n.

$\displaystyle \text{Domino-}n = \{ (a, b) \mid 0 \le a \le b \le n \}$

Consideremos una grilla cuadrada. El objetivo del juego es colocar todas las piezas de dominó en el tablero, con un pequeño twist. Dos piezas pueden superponerse si comparten un número en un casillero dado. Por ejemplo, la siguiente imagen:

Vemos una teselación que contiene los dominós (0,1) y (0,2). Las piezas se superponen en el 0.

Entonces, el objetivo del juego es encontrar para el Dominó-n, una solución con la menor área que contenga todas las piezas del conjunto Dominó-n. O en otras palabras, la mínima cantidad de cuadrados necesarios de la grilla para poner todas las piezas.

En este post, voy a encontrar soluciones óptimas para distintos valores de n.

Complejidad computacional

Recomiendo probar jugar un poco al juego con distintos valores de n. Encontrar soluciones en sí es fácil, pero cuando uno se pone a intentar minimizar el área, se vuelve claro que el problema explota en complejidad a medida que aumenta n y la cantidad de piezas a colocar.

El problema de encontrar una solución óptima tiene dos capas. Por un lado, es encontrar una solución con el área lo más chica posible. Y por el otro, es demostrar que es imposible que exista una solución de área menor. La gran dificultad computacional del problema viene de la segunda parte.

Imaginemos por ejemplo que queremos demostrar que no hay soluciones con área 17 para el Dominó-6. Si quisiéramos probar a fuerza bruta, cada casilla tiene 7 opciones de número distinto, del 1 al 7. Eso ya nos da ~2.3 x 10ˆ14 posibles soluciones, y ni siquiera miramos las posibles configuraciones de los cuadrados en el tablero, que son muchos millones, y se acumulan multiplicativamente.

Como referencia, para dar un poco más de contexto matemático, aunque no sea riguroso. El problema es muy similar a ciertos problemas de coloración de grafos (imaginen que los números son colores, no hay diferencia entre decir 0 1 y 2, o azul verde y rojo).

Es sabido que ese tipo de problema de optimización es computacionalmente “difícil”, en un sentido técnico. Incluso con programas de optimización fuertes, este tipo de problema puede llegar a ser muy difícil de resolver. Es necesario encontrar alguna forma de acotar el espacio de búsqueda.

Resolución

Dividimos entonces la resolución del problema en dos “fases”:

La primera fase, con un enfoque matemático, va a ser la búsqueda de una cota inferior para el área de la solución óptima del Dominó-n. Voy a demostrar que, para el Dominó-n, el área A de una solución debe ser mayor o igual a una cierta fórmula m(n).

La segunda fase, con un enfoque programático, va a ser encontrar soluciones con área m(n) para los Dominó-n con n desde 6 hasta 10 inclusive. Al no poder existir una solución de área menor, queda demostrado que esa es la mínima área posible para el Dominó-n. Hay una leve excepción para el Dominó-7 que explicaré más adelante.

Cota inferior

Recapitulando, estamos buscando una manera de acotar inferiormente el área de una solución S del Dominó-n. Para hacer eso, definamos primero un par de términos y fórmulas auxiliares:

A(S) = Área de la solución S (cantidad de cuadrados ocupados)
Ad(S) = Numero de adyacencias internas de S.
P(S) = Perímetro de la solución S

Explicación rápida del perímetro:

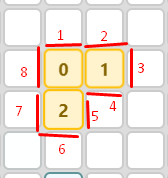
Si consideramos esta figura, el perímetro es 8: La cantidad de conexiones que la figura tiene con casilleros no ocupados.

El número de adyacencias internas es la cantidad de conexiones internas de la figura. Por ejemplo, la figura dada tiene 2 adyacencias internas:

Si consideramos el hecho de que cada cuadrado en la grilla tiene conexiones con 4 cuadrados, tenemos la siguiente fórmula que se cumple para cualquier solución S, que llamaremos Fórmula A:

$\displaystyle 4\,A(S) = 2\,Ad(S) + P(S)$

Es intuitiva de entender: La solución tiene A(S) cuadrados. Cada uno de esos tiene 4 conexiones, dándonos un total de 4 * A(S) conexiones relacionadas a S (el término izquierdo). Algunas de esas conexiones están en el borde de la solución: esas son exactamente el perímetro P(S). El resto, al no estar conectadas con un cuadrado sin rellenar, son una adyacencia interna. Y cada adyacencia interna la tenemos que considerar 2 veces, ya que conectan exactamente dos cuadrados. Esto nos da el lado derecho, 2 * Ad(S) + P(S), dejándonos la fórmula A.

De qué sirve mirar las adyacencias internas: El dominó-6, por ejemplo, tiene 28 piezas de dominó a colocar. Cada pieza de dominó tiene 2 cuadrados. O sea, que por cada pieza que se quiera colocar, es necesaria al menos 1 adyacencia interna en la solución. O sea, para una solución del dominó-6, la forma de la solución debe dar lugar a al menos 28 adyacencias.

Generalizando, la cantidad de piezas a colocar para el Dominó-n es:

$\textstyle \tbinom{n+1}{2} + (n+1)$

Entonces sabemos que, dada una solución S, es necesaria la siguiente desigualdad:

$\displaystyle Ad(S) \ge \binom{n+1}{2} + (n+1)$

Por la fórmula A, sabemos que:

$\displaystyle Ad(S) = 2A(S) - \frac{P(S)}{2}$

Juntando estas cuentas, y despejando A(S), llegamos a lo que llamaremos Fórmula B:

$\displaystyle A(S) \ge \frac{\binom{n+1}{2} + (n+1)}{2} + \frac{P(S)}{4}$

Para refinar esta cota, vamos a buscar acotar el perímetro de una solución S.

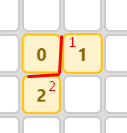
Consideremos R(S), el mínimo rectángulo que contiene a la solución – es decir, el rectángulo de menor área que contiene a toda la figura. Por ejemplo, para nuestra figura:

El cuadrado de 2×2 es el mínimo rectángulo que la contiene.

Dos resultados sobre R(S):

El área de R(S) es mayor al área de S, porque contiene a S.
El perímetro de S es mayor o igual al perímetro de R(S). Esto es un poco más difícil de visualizar, pero viene del hecho de que S tiene al menos 2 bordes por fila y 2 bordes por columna, pero el rectángulo tiene siempre exactamente 2. Queda como ejercicio para el lector convencerse de eso.

Entonces, si consideramos:
w = ancho del rectángulo
h = altura del rectángulo
Tenemos:

$w h \ge A(S) \quad , \quad P(S) \ge 2(w+h)$

Pensemos en todos los posibles rectángulos mínimos de una solución S de área S. Sin pérdida de generalidad, podemos asumir que S tiene un único componente conexo (no tiene piezas sueltas sin conectar), y contemplamos solo un representante de cada clase de simetría.

Entonces queda claro que los posibles valores de w y h son, respectivamente:

$\textstyle w\in\{1,\dots,A(S)\},\quad h=\big\lceil\tfrac{A(S)}{w}\big\rceil,\quad w,h\in\mathbb{Z}_{>0}$

Entonces, combinando todas estas cuentitas, podemos sacar una cota para el perímetro de una solución S:

$\displaystyle P(S) \ge P(R(S)) \ge 2 \min_{1 \le w \le A(S)} \Big( w + \left\lceil \frac{A(S)}{w} \right\rceil \Big)$

Con esto, podemos volver a la fórmula B con más herramientas:

$\displaystyle A(S) \ge \frac{\binom{n+1}{2} + (n+1)}{2} + \min_{1 \le w \le A(S)} \frac{ w + \left\lceil \frac{A(S)}{w} \right\rceil }{2}$

Y reorganizando, nos queda lo siguiente:

$\textstyle 2\,A(S) - \min_{1 \le w \le A(S)} \left( w + \left\lceil \frac{A(S)}{w} \right\rceil \right) \ge \binom{n+1}{2} + (n+1)$

Esto nos da una buena cota inferior para el área de una solución del Dominó-n, y finalmente podemos definir la función m(n).

$\displaystyle m(n) = \min \Big\{ a \in \mathbb{N} \;\Big|\; 2\,a - \min_{1 \le w \le a} \Big( w + \left\lceil \frac{a}{w} \right\rceil \Big) \ge \binom{n+1}{2} + (n+1) \Big\}$

Para cada n, esto nos da la menor área que cumple la cota establecida. Es decir, nos dice que para el Dominó-n, cualquier solución debe tener área mayor o igual a m(n). Algunos valores de m(n):

n	m(n)
5	15
6	19
7	23
8	28
9	34
10	40

Y un gráfico de la función para n de 1 a 100:

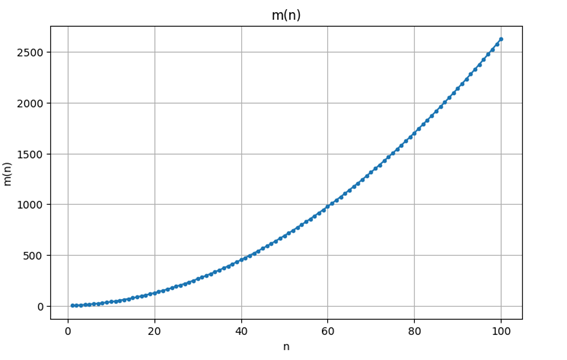
Ahora que tenemos esta cota inferior, si lográsemos encontrar para cada n, una solución de área m(n), sabríamos que es óptima.

Búsqueda de soluciones

Para buscar soluciones, lo planteé como un problema de constraint programming mediante MiniZinc, usando Google OR-Tools como solver. El código puede encontrarse en este repositorio de git, junto a más detalles técnicos del proceso. Todo se corrió en mi computadora de escritorio normal, con las corridas tardando entre pocos segundos a varias horas para los valores de n más grandes. Se usaron estas especificaciones en MiniZinc:

Para casi todos los valores de n hasta 10, existe una solución de área exactamente m(n), es decir, son soluciones óptimas. A continuación, dejo todas esas soluciones para n entre 6 y 10 (las previas son triviales de encontrar).

Una nota: no siempre existe una solución de área m(n) para n. Por ejemplo, m(7) = 23, pero no puede existir una solución del Dominó-7 de área 23 – la más chica es de 24, que en efecto existe. Esto se debe a otra cota combinatórica. Para poder tener una solución del Dominó-7, cada número debe estar conectado a al menos 7 otros números, y a sí mismo. Para esto, son necesarios al menos 3 cuadrados para cada número, dando un mínimo de 3*8 = 24.

Listado de soluciones

n = 6

El valor de m(6) es 19. Existe una solución de area 19, con lo cual es óptima.

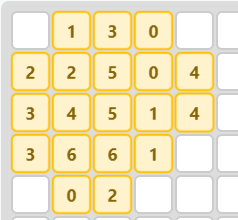
Versión importable:

| 0, 2, 4, 1, 0
| 3, 3, 6, 1, 5
| 4, 5, 6, 2, 5
| 4, 7, 7, 2, 0
| 0, 1, 3, 0, 0

n = 7

El valor de m(7) es 23. No existe una solución de area 23 – 24 es el mínimo por el argumento dado más arriba.

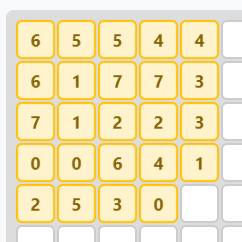
Version importable:

| 7, 6, 6, 5, 5
| 7, 2, 8, 8, 4
| 8, 2, 3, 3, 4
| 1, 1, 7, 5, 2
| 3, 6, 4, 1, 0

n = 8

El valor de m(8) es 28. Existe una solución de area 28, con lo cual es óptima.

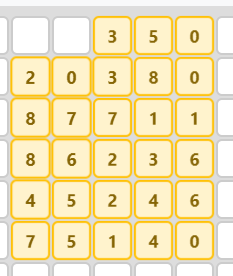
Versión importable:

| 0, 0, 0, 0, 4, 6, 1
| 0, 0, 3, 1, 4, 9, 1
| 0, 0, 9, 8, 8, 2, 2
| 0, 0, 9, 7, 3, 4, 7
| 0, 0, 5, 6, 3, 5, 7
| 0, 0, 8, 6, 2, 5, 1
| 0, 0, 0, 0, 0, 0, 0

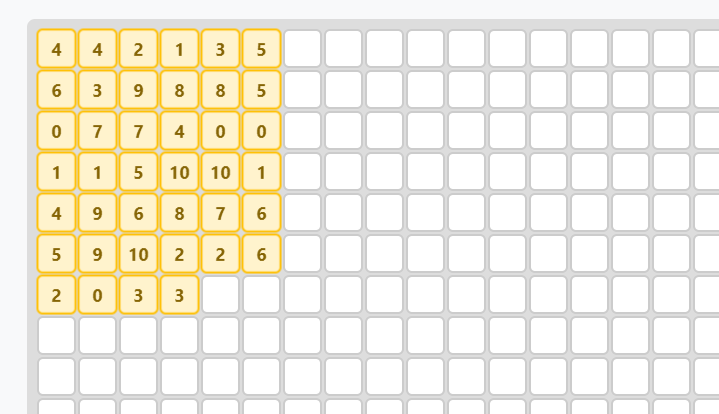
n = 9

El valor de m(9) es 34. Existe una solución de area 34, con lo cual es óptima.

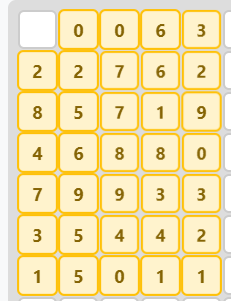
Versión importable:

| 0, 1, 1, 7, 4
| 3, 3, 8, 7, 3
| 9, 6, 8, 2, 10
| 5, 7, 9, 9, 1
| 8, 10, 10, 4, 4
| 4, 6, 5, 5, 3
| 2, 6, 1, 2, 2

n = 10

El valor de m(10) es 40. Existe una solución de area 40, con lo cual es óptima.

Versión importable:

| 5, 5, 3, 2, 4, 6
| 7, 4, 10, 9, 9, 6
| 1, 8, 8, 5, 1, 1
| 2, 2, 6, 11, 11, 2
| 5, 10, 7, 9, 8, 7
| 6, 10, 11, 3, 3, 7
| 3, 1, 4, 4, 0, 0

¿Cómo seguir?

Para valores de n mayores a 10, rápidamente se vuelve muy difícil la búsqueda de soluciones de area m(n). Planteo la siguiente conjetura:

Para todo n ≥ 8, existe una solución del Domino-n de área m(n), y es óptima.

En otras palabras, m(n) no es solamente una cota inferior del área minima, sino que directamente es el área mínima para el Domino-n. Intuitivamente esto parece ser cierto, ya que para valores de n grandes, la cota m(n) es mucho más fuerte que la cota combinatorica que le “gana” para n = 7. De todas formas, todavía no encontré la forma de demostrarlo. No parece haber una manera fácil de construir soluciones a partir de soluciones más chicas, u otras herramientas similares.

Otro experimento interesante sería tratar de encontrar soluciones óptimas para los Domino-n con n entre 11 y 20, que parece computacionalmente alcanzable si se le dá el suficiente tiempo.

Dominó Compactado: Soluciones Óptimas

Formulación

Complejidad computacional

Resolución

Cota inferior

Búsqueda de soluciones

Listado de soluciones

n = 6

n = 7

n = 8

n = 9

n = 10

¿Cómo seguir?

One Comment

Deja un comentario Cancelar respuesta